Boness 1964 Option Pricing Formula [Loxx]

Oct 4, 2022

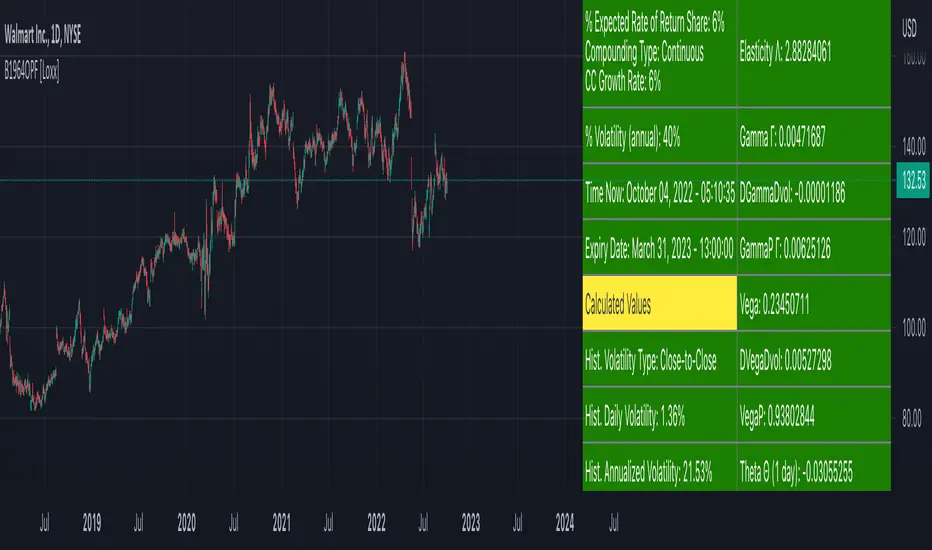
Boness 1964 Option Pricing Formula [Loxx] is an options pricing model that pre-dates Black-Scholes-Merton. This model includes Analytical Greeks.

Boness (1964) assumed a lognormal asset price. Boness derives the following value for a call option:

c = SN(d1) - Xe^(rho * T)N(d2)

d1 = (log(S / X) + (rho + v^2 / 2) * T) / (v * T^0.5)

d2 = d1 - (v * T^0.5)

where rho is the expected rate of return to the asset.

Analytical Greeks

• Delta Greeks: Delta, DDeltaDvol, Elasticity
  
• Gamma Greeks: Gamma, GammaP, DGammaDvol, Speed
  
• Vega Greeks: Vega , DVegaDvol/Vomma, VegaP
  
• Theta Greeks: Theta
  
• Probability Greeks: StrikeDelta, Risk Neutral Density, Rho Expected Rate of Return
  

Inputs
S = Stock price.
X = Strike price of option.
T = Time to expiration in years.
r = Expected Rate of Return
v = Volatility of the underlying asset price
cnd (x) = The cumulative normal distribution function
nd(x) = The standard normal density function
convertingToCCRate(r, cmp ) = Rate compounder

Things to know

• Only works on the daily timeframe and for the current source price.
  
• You can adjust the text size to fit the screen