GVWAP_Core (CalendarSpan + EventSpike)

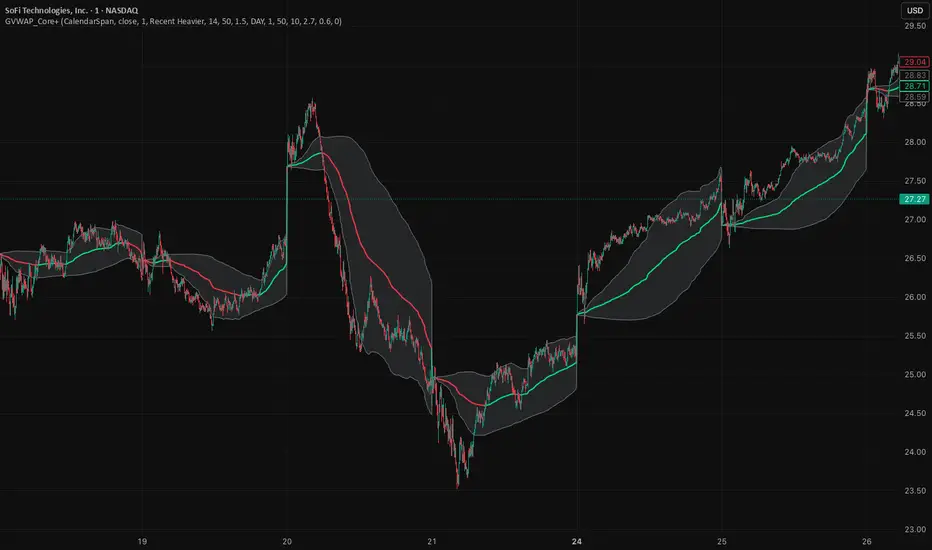
GVWAP Core Indicator

General Description (Public)
GVWAP (Generalized Volume-Weighted Average Price) is an advanced anchoring and averaging framework designed to reveal market structure rather than predict price. Unlike traditional VWAP, GVWAP is not limited to volume weighting or session-based anchoring. It can operate on any input series (price, indicators, transforms) and supports multiple weighting schemes, decay behavior, and structural reset logic.

At its core, GVWAP answers a simple question: “Where is the statistically relevant center of activity since the last meaningful structural event?”

The indicator continuously updates a weighted average of the input series, gradually forgetting older data using exponential decay. The anchor point can reset on calendar boundaries (day, week, month, etc.) or on statistically significant events such as abnormal volume spikes. Robust dispersion bands based on mean absolute deviation (MAD) surround the average, providing context for trend, rotation, and compression regimes.

GVWAP is not a trading signal by itself. It is best used as a structural reference layer or as an intermediate transform feeding other indicators, strategies, or regime filters.

Mathematical Description (Quantitative)
Let x_t be an arbitrary input series and w_t a selectable weight function. GVWAP is defined as a normalized exponentially decayed weighted estimator:

GVWAP_t = N_t / D_t

with recursive updates:

N_t = (1 − α)·N_{t−1} + α·w_t·x_t
D_t = (1 − α)·D_{t−1} + α·w_t

where α = 1 − 2^(−1/H) and H is the decay half-life in bars.

Weights may be defined as:
• w_t = V_t (volume)
• w_t = 1 (equal weight)
• w_t = 1 / ATR_t (volatility-normalized)
• w_t = f(n_t) (time-weighted, where n_t is bars since reset)

The estimator resets when a structural condition R_t is satisfied, at which point:

N_t = w_t·x_t, D_t = w_t

For event-based anchoring, volume surprise is computed using a Student‑t–compressed z‑score:

z_t = (V_t − μ_V) / σ_V
tZ_t = z_t / sqrt(1 + z_t² / ν)

A reset occurs when tZ_t exceeds a threshold τ.

Dispersion is measured via a decayed Mean Absolute Deviation:

MAD_t = (Σ λ^{t−i} w_i |x_i − GVWAP_t|) / (Σ λ^{t−i} w_i)

Bands are defined as GVWAP_t ± k·MAD_t.

GVWAP therefore represents a bounded-memory, robust, non‑Gaussian estimator of the local conditional expectation of x_t under dynamic anchoring and weighting.